Today we'll dive into the heart of the matter and tackle the different modes, major and minor (natural, melodic and harmonic), as well as the relative scales.
The Major Mode
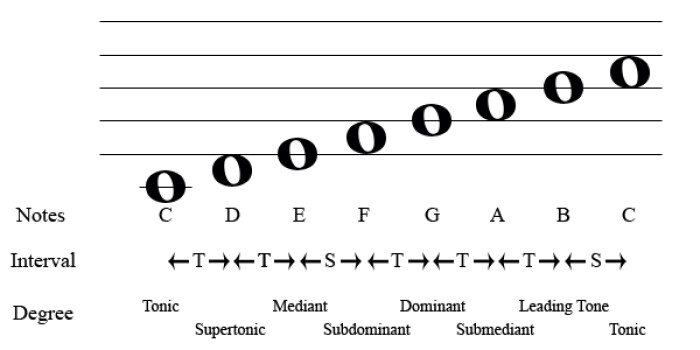
Here’s how a major scale is constructed:
1 tone + 1 tone + ½ tone + 1 tone + 1 tone + 1 tone + ½ tone
If you do the math, everything is squared away: there are 12 semitones and eight notes. Every major scale is therefore made up of certain specific notes. Furthermore, each element of a major scale has a degree and a function within the scale.
As you can see in the example, D is the second degree of the C-major scale and it has a supertonic function. We’ll see what these functions are all about in a future article.
Relative Scales
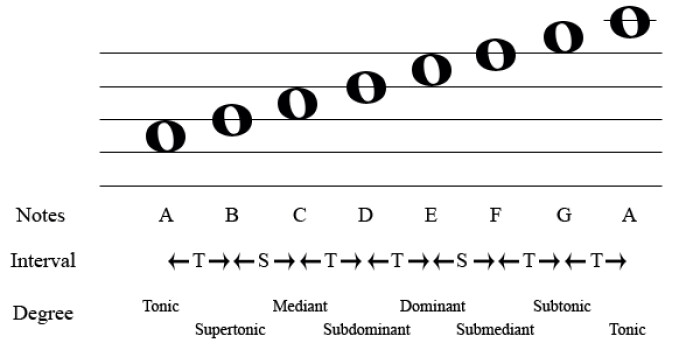
From the previous example it’s easy to tell that the C-major scale has no accidentals (no sharp nor flat notes, it uses only the white keys of a keyboard). But there’s also a minor scale that uses the exact same notes: A-minor, whose tonic or key note is located exactly one-and-a-half tones below the tonic of the C-major scale.
Two scales that share the same notes and whose key notes are located one-and-a-half tones apart are called “relative” scales or keys. Every major scale has its own relative minor, and vice versa.
The Minor Mode (and its three odd scales)
As if things weren’t complicated enough as it is, the minor mode does not have one single type of scale, like the major mode ─ it has three. Let’s take a closer look at them.
The relative minor of a major scale is called the “natural” minor. But be careful, the fact that the tonics are one-and-a-half tones apart doesn’t necessarily mean that all other notes are! If that were the case, the relative minor of a major scale would be…another major scale! Here’s how a minor scale is constructed:
1 tone + ½ tone + 1 tone + 1 tone + ½ tone + 1 tone + 1 tone
Once again, if you do the math, you’ll end up with 12 semitones and 8 notes (7 + the tonic one octave above where it started). The first big difference with a major scale is that the third degree, starting from the key note, is now a minor third. The other big difference with the major scale is that the second semitone is not between the 7th and 8th degrees anymore, but rather between the 5th and 6th degrees. So, the last interval is a whole tone, not a semitone. There is no leading-tone anymore, which means the sensation of something resolving ─ like with the final semitone ─ isn’t there any longer.
Incidentally, the second type of minor scale ─ called harmonic minor ─ was born from the desire some people had to replicate this resolution produced by the final semitone. And thus came to be the harmonic minor scale.
1 tone + ½ tone + 1 tone + 1 tone + ½ tone + 1 tone-and-a-half + 1/2 tone
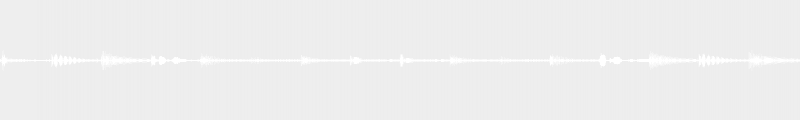
However, some other people argued that the one-and-a-half-tone interval between the 6th and 7th degrees was too big, and a little disturbing to the ear. So they decided to reduce it by raising the 6th degree one semitone. And that’s how the third type of minor scale, the melodic minor scale, developed. You could say it begins like a minor scale and ends like a major scale.
This is what it looks like:
1 tone + ½ tone + 1 tone + 1 tone + 1 tone + 1 tone + ½ tone
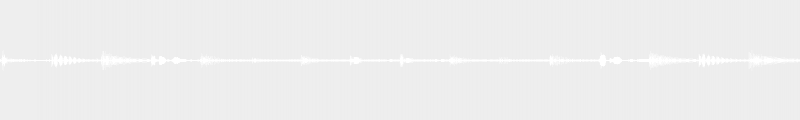
Do note however, that while the melodic minor “works” when ascending from the lower notes to the higher ones, it sounds odd when it goes the other way around, because the ear is expecting a major scale. That’s why you usually use the natural minor when descending, which is why it is sometimes called the descending melodic minor scale, as you can hear in the following example (with the ascending melodic minor and descending natural minor):

In the next article we’ll see how to determine the overall key of a song.