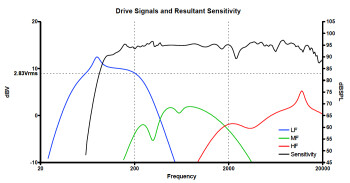
Knowing how much power a speaker can handle doesn't tell you anything about how much SPL it can deliver.
Part of the signal’s energy is dissipated along the way. In a classic loudspeaker, the signal makes the voice coil move in a magnetic field, setting the diaphragm in motion to modify air pressure. Unfortunately, a good share of the energy disappears in the form of heat when passing through the coil and magnets. Transforming electrical energy into mechanical and then acoustical energy entails, more or less, the significant loss of part of it, depending on the speaker and its enclosure. So, to be able to compare two speakers, you need to know how much SPL they can deliver with the same electric power.
A definition
The sensitivity of a speaker indicates the SPL it can deliver, under test conditions, depending on the power it receives. It is specified as sound pressure level (dB SPL) referenced to an input of 1 watt (1W), or 2.83 volts, or even less, at 1 meter (1m) on the reference axis.
The notion of efficiency is similar, conceptually speaking: it expresses the relation between output power delivered and the electrical power received. It is expressed in terms of a percentage or ratio (10% corresponds to a ratio of 0.1). The efficiency for most speakers is below 5%. Air resists rather well the action of a speaker.
Considering that doubling the electrical power makes the SPL increase in 3dBs, a speaker featuring a sensitivity of 92dB / 1W @ 1m amplified with an input power of 100W will deliver an equivalent SPL to a speaker whose sensitivity is 95dB / 1W @ 1m fed with an input power of 50W. From this it’s easy to tell that knowing the power handling of a speaker without its sensitivity doesn’t allow you to determine the volume it will produce. On the other hand, if you have both, you can determine what is the theoretical maximum level it can deliver.
Why 2.83 volts?
Power (in watts) depends on impedance, which changes with frequency. So, in order to hold a constant power of 1W during the test, the signal voltage needs to be adjusted according to the speaker and the frequency range tested. And, to make things easier, it’s better for the variables to depend on the speaker being tested, not on the signal. So, instead of characterizing the test signal by its power (1W), which is nothing but a value derived from the voltage, it’s better to use a fixed voltage value (2.83V) and measure what the speaker can deliver with that.
The relationship between power (P) and impedance (Z) is P = U2/Z. With 2.83V and an impedance of 8Ω, you get 2.832 V / 8Ω = 1W. For 4Ω: 2.83V yields 2 W. So, a speaker with a nominal impedance of 4Ω will be more efficient if it can deliver 92dB / 1W @ 1m than if it delivers 92dB / 2.83 V @ 1m (in which case it receives 2W). You could say that the use of a 2.83V rating “favors” 4Ω speakers, since they receive more electrical power than 8Ω speakers at the same voltage. So, besides the rating in the form “xdB / 2.83 V @ 1m, ” you should always take into account the Impedance. The more rigorous logic of the rating in volts is favored to the expression in watts, but, as you will see, there are equivalents between both of them.
Maximum level
On some speaker spec sheets you can find a maximum sound pressure level rating (in dB SPL). Which is nothing more than the peak level obtained with the maximum amplification power (specified by the manufacturer). And it can be calculated if you have the speaker’s sensitivity and the power of the amplifier. It is often provided to facilitate the modeling of a system in a real situation. With this figure and a bit of knowledge of the decibel scales, it’s easy to estimate the theoretical SPL you’ll get depending on the distance to the speaker. The short, and simplified, version estimates that you lose 6dB whenever you double the distance (with a spherical wave). This allows you to determine the maximum SPL the listener will be exposed to depending on the distance to the speaker.
**Attenuation, in decibels, depending on the distance to the source, in meters.