In the previous article we saw that sound is made of waves. Like many things in life, they can be simple or complex. You can't find an absolutely "pure" sound in nature. The closest to that is the sound of a tuning fork or the sound emitted, under certain conditions...by a sound synthesis instrument! Now you get why I'm talking about all this, right?
A sine wave, like the one pictured in the last image of the previous article, is a “simple” wave. As soon as you add a non-identical wave to a simple wave, it will turn into a “complex” wave. Oh, yes, if you think about it, that means that whatever the number of sound sources registered at a given time ─ imagine for example an entire symphony orchestra, and don’t forget about the acoustic reverberations of the venue, nor the lady who sneezes to your left and the gentlemen who snores to your right ─ the graphic representation of the recording shows only a complex wave, made up of so-called periodic waves (music notes, as we will see below) and non-periodic sounds (the sneeze and the snoring, for example).
In case you didn’t know, we owe this brilliant discovery to the great mathematician and physicist Joseph Fourier (1768–1830): All complex waves can be decomposed into a certain number of simple sine waves, except for transients, which are the periods when a sound occurs and disappears.
All right, up to now we have made reference to the amplitude and period of the waves…But what are they exactly?
Length does matter!
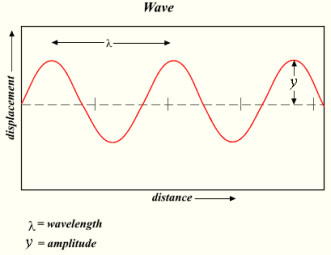
The main properties of a simple sound wave are its amplitude, period, wavelength, phase, and frequency (we will dedicate the entire next article to frequency).
A wave that propagates in a given medium leads to pressure variations in the medium (or, to be more precise, compression and rarefaction). These variations are represented by amplitude and are expressed in Pascals.
Imagine a guitar string. When at rest, it is in “equilibrium.” If you make the string vibrate, it will be displaced up and down from its initial position before coming back to a rest. The amplitude of the movement of the string represents the difference between its maximum displacement in a given direction and the rest position.
The amplitude of a wave represents the difference between its point of equilibrium or baseline, and the maximum level of compression (peak) or rarefaction (trough) exerted on the environment.
Graphically, the baseline is represented by a horizontal axis. The latter represents a vibration level equal to zero, in other words it’s how the wave would look if it didn’t vibrate, if no sound was produced. As a consequence, the farther the peak or trough is from the baseline ─ the more the outline of the wave moves away from the horizontal line ─ the higher the volume of the sound. Thus, the amplitude of the sound wave is directly related to the volume of the sound in question, and it is expressed in decibels (dB). In our example, the greater the displacement of the string between the baseline and its highest or lowest point, the more significant is the amplitude movement and the louder the sound!
Do note that the power of a wave ─ it’s amplitude, that is ─ decreases with time when it propagates in free space, because the energy of the wave is dispersed into the space.
All acoustic instruments have a sound box or a pipe that allows them to reduce the dispersion of the sound wave into the surroundings and, thus, diminish the loss of power. In sound synthesis, there’s no need of a sound box because you can affect the wave directly and make sound last indefinitely, as we will see.
If a simple waveform repeats in time, it’s called “periodic, ” because it’s made up of recurrent cycles. The “period” is the time the waveform needs to complete a full cycle. For its part, the wavelength represents the distance between two cycles of the same waveform.
In phase
Finally, before we move on to frequency in our next installment, here’s a final word on phase. Without going into trigonometrical details that are somewhat off-topic, you must know that phase is measured in degrees and, as far as a musician is concerned, it is defined by the deviation of one wave with respect to another one.
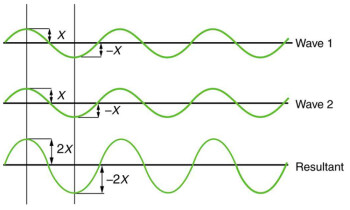
I’ll explain myself: If you mix two absolutely identical waves, 1 and 2, but you make wave 2 start with a 90º offset from wave 1, then these waves are 90º out of phase.
What does it mean that the waves are out of phase, In terms of sound?
Phase can affect sound in different ways. The amplitude of two waves are summed. As we saw before, the volume of a sound depends directly on the amplitude of a wave. If you mix two sounds that are “in phase, ” the positive sides of the waveforms are summed together, and the same happens with the negative sides. This results in the sound being twice as loud.
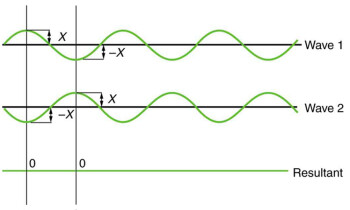
On the contrary, if you mix two sounds that are completely “out of phase, ” the negative side of one waveform will cancel the positive side of the other one and vice versa, resulting in a wave with zero amplitude, in other words, absolute silence!
Obviously, there are lots of possibilities between these two extremes. It’s worth noting that in-phase and out-of-phase waves are the principle underlying some effects that you probably have already experimented with, like phaser and flanger.