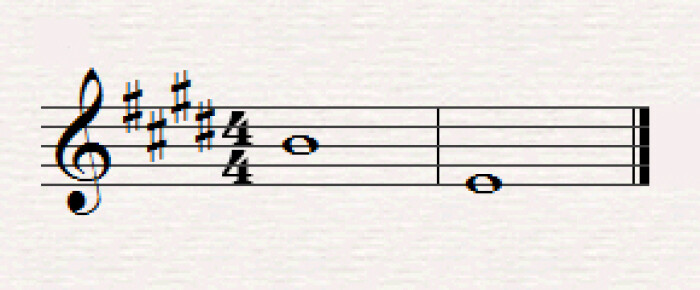This is one of those situations no composer can escape...and the reason for being of this series.
You’ve found a musical phrase that sends shivers down your spine. What’s more, you are convinced that it’s THE melody that will move the hearts of the people all around the world. The only problem is that, as electrifying as it is by itself, it lacks substance and fullness. Wouldn’t it be nice if it were a bit fatter? That’s where harmony comes in with its favorite weapon: chords (we won’t look into counterpoint just yet). But you can’t simply throw in any chord at random. As we’ve seen in the previous articles, not only can every note of a scale (the key of a song) be harmonized with a chord, every single one of them has a specific function, too. That’s what we are going to tackle today.
Degrees
When you decide to harmonize a song, you shouldn’t necessarily add a chord to every note in the melody, otherwise you risk ending up with something that’s everything but harmonic! So you need to do it with good judgment. After determining the key of a song (see article 3), the second step to harmonize the latter is to identify the function of the different notes in it.
In the tonal system, the first (I) and fifth (V) degrees are the main degrees of a scale (all others depend more or less on them, as we will see in a future article). The first degree of a scale is called the “tonic, ” since the “tonality” (or key) revolves around it. The fifth degree, called dominant, is there to reinforce the character of the key. In fact, to the “western” ear, every note is attracted to the one that’s a perfect fifth below it, due to a psychoacoustic effect. Try it yourself. Play a note, any note, and follow it by the one that’s a perfect fifth below (three tones and a half, that is, according to article 1): you will immediately feel it resolving, or coming to an end. In this case, the second note you played would be the tonic of the key. The dominant would be the first note you played.
.
This movement from the fifth towards the first degree of a scale is called perfect or authentic cadence (from the Latin “cadere, ” to fall). This formula is very commonly used to finish a song. So, in many cases, the two degrees used to finish a melody of a song are the dominant (or one of the notes that make up the dominant chord, as we’ll see shortly) and the tonic (or one of the notes of the tonic chord). There are many other cadences and each of them has a very specific role in the composing and harmonizing of a song, which is something we’ll see in a future article, too. For the time being, let’s focus on the study of the degrees of a given key.
After the I and V degrees, the third most important one is the fourth (IV), called subdominant. Its function is to reinforce the V degree. Many songs feature a subdominant chord preceding the perfect cadence (V-I).
Below are two examples of the IV-V-I cadence. First are the “naked” degrees and then with a basic harmonization:

If you recall the previous article, you’ll be able to notice two things regarding the chords that correspond to the I, IV, and V degrees of a major scale. The first one is that they are all major. The second one is that, between them, they make up all the notes of the scale, as you can see in the following example:
This means that you can basically harmonize any “classic” western song using only these three degrees.
If you recall article 3 of this series, you will also realize that the IV and V degrees are neighbor tones of the tonic. They are placed right and left of the tonic in the circle of fifths. This makes it very easy to identify the IV and V degrees of any scale, and thus begin harmonizing any song, regardless of the tonic.
In the next article we’ll study the rest of the degrees of a scale and will also look briefly into harmonization in the minor mode.